【印刷可能】 慣性 モーメント 円盤 370963-円盤 切り抜き 慣性 モーメント
まず円盤が質点の集まりで出来ていると考え, その円盤の中の小さな一部分が持つ微小な慣性モーメント を求めてそれを全て足し合わせることを考える つまり, 式で書くと全慣性モーメント は次のように表せるということだ この積分記号 は全ての を足し合わせるという意味であり, 数学の · 円板の慣性モーメント 以下のような円板の慣性モーメントを求めます 質量はm、密度はρとし、tは非常に小さいものとします まずは円板に垂直な軸まわりの慣性モーメントから求めます、円板に垂直な方向から見た図を考えて 上図の微少な幅drの質量dmは d m = ρ 2 π r d r = m π R 2 2 π r d r = 2 m r R 2 d r 積分範囲は0~Rである よって慣性モーメントは I z = ∫ 0 R r 2 ⋅ 2慣性モーメントとGD2の関係 慣性モーメントとGD2の換算 GD2に おけるDは、回転半径に対する回転直径のようなものであって、 k が回転体の半径そのも のではないように、Dも回転体の直径そのものを表わしているのではない。 慣性モーメント I は、物体の質量 m と回転半径 k によって表わすこと
一様な物質でつくられた半径a 質量mの薄い円板がある 円板の中心からa Yahoo 知恵袋
円盤 切り抜き 慣性 モーメント
円盤 切り抜き 慣性 モーメント-よって円盤の密度をρkg/m 3とすれば、この欠片の重さはρ・r・dr・dθ・dzで表されます。よって慣性モーメントの定義式より、慣性モーメントは と求まります。 慣性モーメントの例 いくつか代表的な形状を挙げ、その慣性モーメントを記載します。Mはタイムテーブル慣性モーメントの物理的意味 1~質点の慣性モーメント 336~円運動におけるv=rωの証明 415~大きさをもつ物体の慣性モーメントの
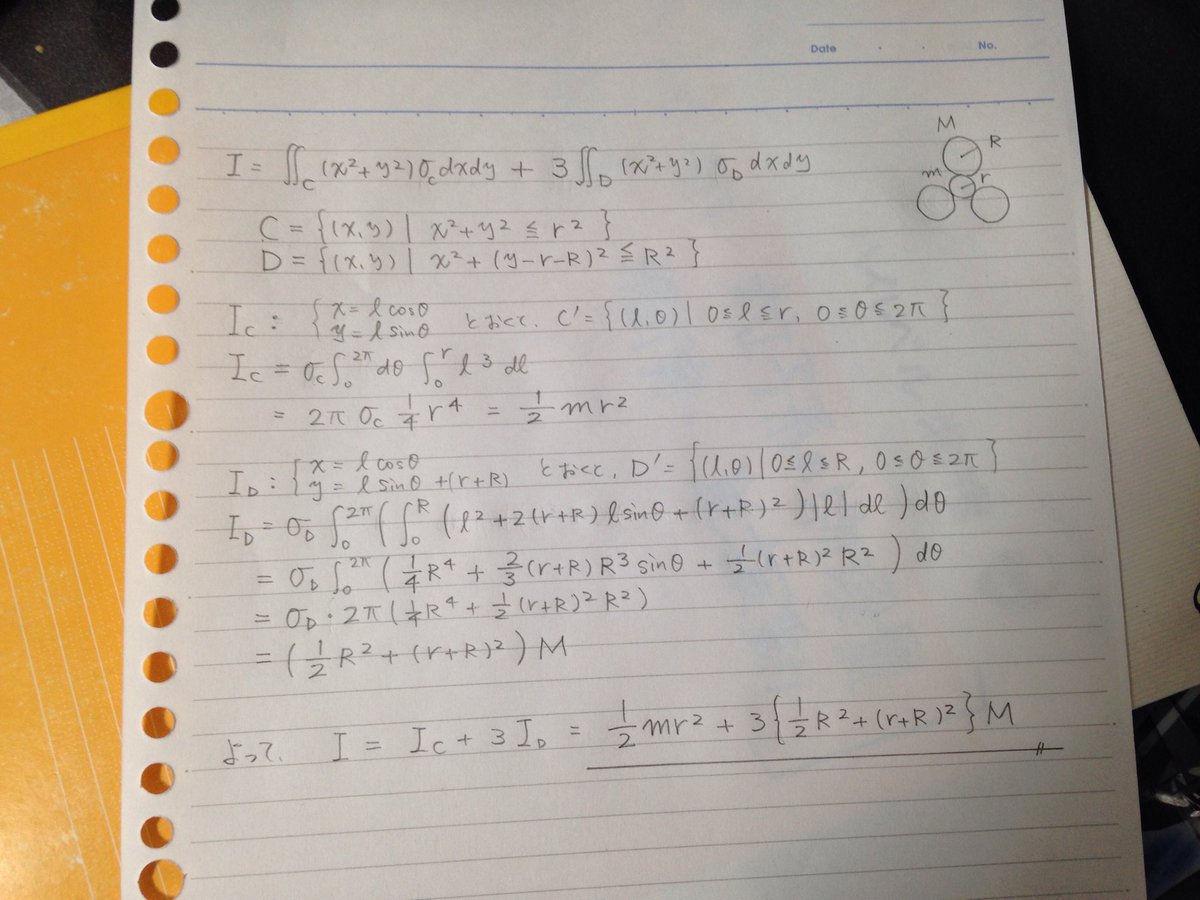


結数 ゆず على تويتر はい 等質量の円柱と円盤の慣性モーメントが等しいので ハンドスピナーを円盤の組み合わせに見立てました なのでsは面密度ですね 数学ガール大好きでいつも楽しませて頂いてます
図2 OP を軸とする (文責・生出)間違っているところがあれば,指摘してくれるとありがたいです. 4 Created回転軸が重心を通らない場合 (2)直線運動の慣性モーメント(負荷側軸における慣性モーメント) ※図をクリックして下さい。 一般用途 コンベアによる水平運動;10.4 慣性モーメントに関する2つの定理 10.5 慣性モーメントの計算例 10.6 簡単な剛体の運動 剛体振り子: 右図のように重心からaだけ離れたO点を 軸とした長さ2l 質量Mの棒の振動を考える。 1.O点回りの慣性モーメントは半径aの公転と 中心回りの自転の慣性モーメントの和である。 2.力の
慣性モーメント ∑ × − ∆ = M (x a) 2 L x I 2 2 12 1 = ML Ma 結果の解釈 重心のまわり (a=0 のとき) の 慣性モーメント 2 12 1 I G = ML 左の結果 I Ma 2 = G 平行軸の定理 一般化 a は重心 からの距離 分割和から積分へ ( p16 :基本パターン) = ∫ − − 2 2 2 / / L L x a dx L M I慣性モーメントI I r dm 剛体 2 r 2 r y x 幅dr R2 M 円環 円盤 dm dV 2 r dr r dr R M R M R 0 3 0 2 2 2 2 円周 薄い円盤の中心の周りの慣性モーメント (質量M、半径R) 問26 𝐼 ±𝑟 6 𝜌 Ìd𝑆 剛体 Ì L 𝑀 𝑆 単純な形状の物体の回転運動 回転軸 x 0 l 慣性モーメントI円盤の質量が与えられていれば厚さ d は慣性モーメントに関係しませんが、円盤の質量を密度と体積から求めるならそこに厚さ d が関係しますので、慣性モーメントにも厚さ d が関係することになりま
5 1(g· cm2) の慣性モーメントは,何(kg· m2) に相当するか. 6 図1に示すように,円盤がベアリングを介して軸に取り付けられている.円 盤は軸の回りに回転することができる.円盤の慣性モーメント第1法則;外から力を受けない物体は,静止しているか等速直線運動を続ける(慣性の法則) 第2法則;物体に力を加えると,物体にはその質量に反比例した加速度が生じる(ニュートンの運動方程式) 第3法則;物体Aが物体Bに力を加えているとき,物体Aは物体Bから同じだけの力を受ける(作用・反作用の法則) 特に,第2法則について述べたいと思います. 質量を慣性楕円体 慣性モーメントIαβ が与えられたとき、3次元空間において、次の式で表される楕円 体を、慣性楕円体と呼んでいる。 ∑ αβ Iαβxαxβ = Ixxx 2 I yyy 2 I zzz 2 2(I xyxy Iyzyz Izxzx) = 1 (510) 慣性主軸に対応する固有ベクトルを座標軸とする座標系においては、上の方程式は以下の形に表さ


一様な円盤の慣性モーメント



ヨーヨー力学その39 回転方向以外の慣性モーメントと傾き安さ 趣味を科学する
上で求めた細い輪の慣性モーメントを利用して円盤の慣性モーメントを求める。半径 の微小な輪の慣性 モーメント を積分する。 面密度 円盤の質量 x z y R /°2 M 図 半径 で質量 の円盤の慣性モーメントを考える。 半径 の薄い球殻 も同様だから x z R y /°2 M 図穴あき円盤の慣性モーメント 密度ρ=78 ton/m^3、半径R= cm、厚さt= mmの円盤に、半径r=10 cmの位置に中心点を持つ直径D=8 cmの穴が90°間隔で4個空いてる円盤の中心軸(長て方向)周りの慣性モーメントIoの計算が上手くいきません。 先ず穴があいてない円盤の質量m1・慣性モーメントIo1を求めて、次に平行軸の定理から穴をあけた分の質量m2・慣性モーメントIo2を)このような回転系の慣性モーメントはいくらか。 I x = I y = 1 2 m 2 =195×10−46kg m2,I z =0 1342 円盤 半径a、質量M の厚さが無視できる円盤がある。円盤の中心を通る円盤に垂直な軸の周りの 慣性モーメントは I = ρr22πrdr= 2π 4 ρa4 = 1 2 Ma2



計算 換算表 Pmステッピングモーター 小径 高速 技術解説 Eminebea



慣性モーメント 円柱が段差を乗り上げる条件 プログラミング日記
03 · 円柱の慣性モーメントについてですが、これは先ほど円盤の慣性モーメントを計算したので、その結果を使って計算していきたいと思います。 薄い円盤の慣性モーメントは\(\frac{1}{2} m_{1} R^2\)でした。これが高さ\(h\)分積み重なったとものが円柱の慣性モーメントと考えることがで慣性モーメント:一般論 慣性モーメントはいくつあるのか?無数? 1)重心を通らない回転軸の I は,重心を通 る平行な軸に関する I から決まる。 (p84平行軸の定理) 2)重心を通る任意の軸に関する I は3つの 主慣性モーメントから決まる。 (514節:慣性テンソル) → 以下で説明と慣性モーメントが求められる。すなわち 地球や月の慣性モーメントはこうして求められたものである。適当な成層構造を仮定すると のみから慣性 モーメントを推測することも可能である。ガリレオ衛星の慣性モーメントは衛星のフライバイに伴って計測


慣性モーメントについて図の円盤の慣性モーメントの計算方法について教えてください Yahoo 知恵袋



慣性モーメントに関する質問 勉強質問サイト
慣性モーメント・GD2 慣性モーメント・GD2と始動時間 相手機械を完全に始動させるためには、始動トルクが負荷トルクより充分に大きく、また動き始めてから全負荷速度に達す るまでの間もモータトルクが常に負荷トルクを上回っていなければなりません。 始動期間中のモータトルクと負荷トルクとの差が加速トルクで、平均加速トルクをTa(N・m,kgf・m)とすると円盤の対称軸に関する慣性モーメントの計算 Ⅰ-半径 、質量が の円盤を考えます。 この円盤の中心を通りその円盤に垂直な軸のまわりの慣性モーメントを求めてみましょう。 まず座標系は2次元の平面極座標としてとらえます。 この時の微小部分の面積はヤコビアンの計算 により さらに全質量が 、面積が であるので円盤の密度 は よって微小部分の質量は一様な円盤の慣性モーメント 一様な円盤(質量M、半径a)の中心軸まわりの慣性モーメントを実際に求めてみる。 一様な円板の中心軸まわりの慣性モーメントを求める 図を書くと、 慣性モーメントは、こちらで解説したので問題なし。円板の面密度を ρ とすれば、


2 7 慣性モーメント 回転運動は落下運動と形式的に同じであり A A V W M 質量 M に相当するものは何であろうか 今 はずみ車 子供の玩具に利用され 車を床に置いて動かしてのタイヤを回転させて手を離すと床を走る の回転を


慣性モーメント 例題 H23 1 1 Occasion Hill 学術
に慣性モーメントが求まるので実験結果と比較できる.しかしながらこれを確かめるには正確な時間とふれる 2/8 x4 重心が中点からずれている場合 回数を測定しなければいけないので煩雑である.よってもっと簡単に確かめることを試みよう.長さ2b の一 様な太さの棒の慣性モーメントは J慣性モーメントの計算法 対称形の物体の慣性モーメント 形状にはさまざまなものが考えられるが、特別なものを除いて一般にいくつかの基本的な形状、円柱や直方体たどを組合わせて構成されていると仮定し計算する。 1 ) 円柱(円板) 右図に示すような円柱を考え、 回転軸を2軸として慣性以下に慣性モーメントの計算でよく用いる物体とその計算式を示します。 なお、J (kgfcmsec2) =I (kgm2) × 102の関係があります。 図①の様な回転中心を持つ質点の慣性モーメントは、次式とな ります。これは、xが物体の大きさに対して十分大きいとき に 近似値として使えます。 図⑤ の様 円柱
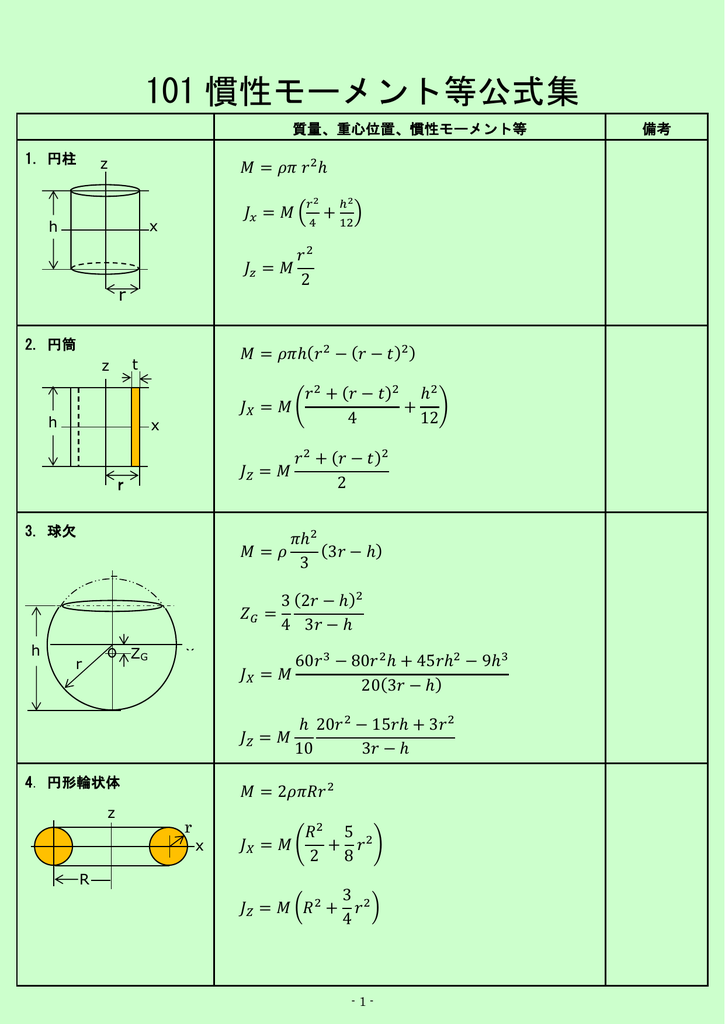


球 慣性 モーメント Article



3 から教えて欲しいです Clear
· 円板の慣性モーメントが 1 2 M a 2 \dfrac{1}{2}Ma^2 2 1 M a 2 であることは認めます。 証明 球の中心が原点,回転軸を z z z 軸とする座標で考える。 z z z 座標が z z z から z d z zdz z d z の間にある部分は薄い円板とみなせる。 その半径は, R 2 − z 2 \sqrt{R^2z^2} R 2 − z 2 ,質量は h o S d z = h o π (R 2 − z円環 慣性モーメ L IIM ント R2 慣性モーメント I MR2 5 質量Mkgの円盤の角運動量 半径r 微小角度d ラジアンの回転 d R 密度 微小パーツの体積(→面積)を求める LrdV II 慣性モーメント 2 r d dr rd rd dr = 微小パーツの面積=dS慣性モーメント 高杉 計算方法 慣性モーメントは I = ρr′2dV ここでr′ は回転軸からの距離である。 質量密度をρとすると、質量は M = ρdV で求められる。体積要素は dV = dxdydz (直交座標) = rdrdθdz (円筒座標) = r2 sinθdrdθdϕ (球座標) である。



慣性モーメントj Kg M 2 の計算式 技術資料 オリエンタルモーター株式会社
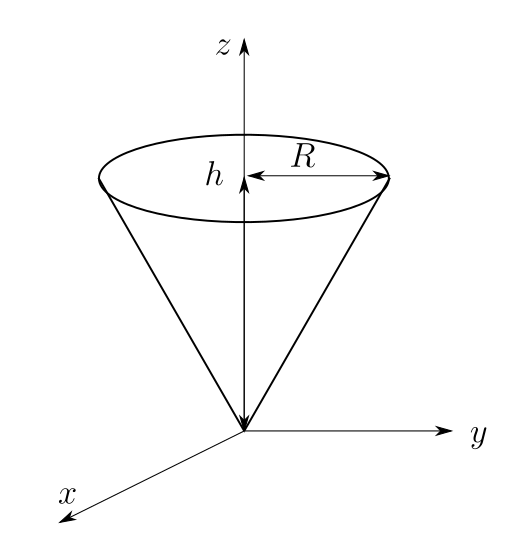


円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目
のことを指します.逆に言えば,慣性モーメントというのは考えている剛体について,どの方向を軸とするか を指定してはじめて意味を持つものと言えます. 7 0 Y Z 1 S T!大学物理 円盤の慣性モーメントと円筒の慣性モーメントが同じ形になるのはなぜですか?教えてください。 教えてください。 ベストアンサー:「円筒」というと、 普通は中空で穴のあいた円い筒を指すことが多いと思いますが、 あなたが言いたいのは「円柱」のことではないでしょうか。一様な球の慣性モーメント 一様な球(質量M、半径a)の中心軸まわりの慣性モーメントを実際に求めてみる。 一様な球の中心軸まわりの慣性モーメントを求める 図を書くと、 今回の問題を解く方法としては、zとzdzに挟まれた円盤(要するにdzの幅で輪切りにした円盤)の慣性モーメントを



円板の慣性モーメントを求める計算の途中の疑問 半径a 質量mの一様 物理学 教えて Goo



電気磁気工学を学ぶ 円板の慣性モーメント
慣性モーメント (1)回転体の慣性モーメント ※図をクリックして下さい。 回転軸が重心を通る場合;求めるとき、質量M半径aの円板の慣性モーメントがMa^2/2であることを利用して、中心軸zの円板の慣性モーメントを足し合わせるやり方で ∫ (aからa)πσ (a^2z^2)^2/2 dz とすることで2Ma^2/(4)慣性モーメント 以下に示す例は重要である。いずれも対照的な形状で、回転軸がその重心を通り、物体の各部分の密度は同じで一様とする。全質量をMとして図中のx、y、z軸の間まわりの慣性モーメントI x 、I y 、I z の値を示す。



3 3慣性モーメントを計算する
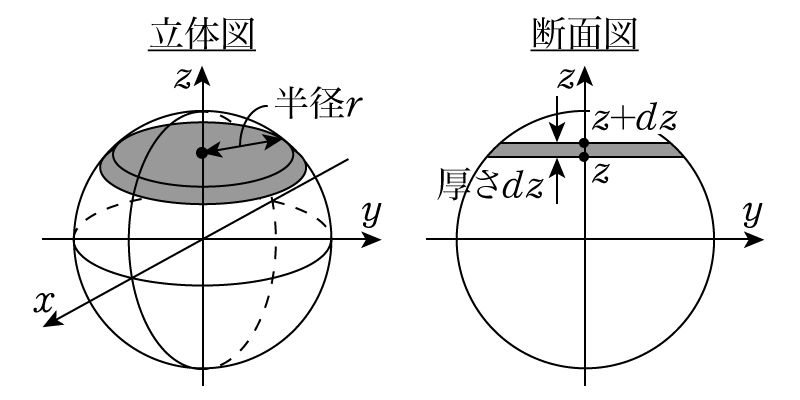


剛体の慣性モーメントの計算 物理の学校
O点のまわりの慣性モーメントを求めるので、平行軸の定理でh=b/2として、 1)糸が切れたとき、張力Tがなくなり、棒は棒の重心に働く重力Mgによって反時計回りに回転を 始める。このとき、力のモーメントは、 N=Mg・b/2・sinθ よって、回転の方程式は、 f £mN q q1慣性モーメント算出 2慣性モーメント加速度・減速度の確認 〈慣性モーメント加速度・減速度グラフ〉 を参照し、慣性モーメントと加速度・減速 度から対象機種を選定してください。 ロータリータイプ:RF03 取付姿勢:水平 負荷の種類:慣性負荷 Ta 負荷の形状:150mm×80mm(長方形板) 揺動6 球の慣性モーメント 半径R,密度(単位体積当り質量)ρの球の慣性モーメン トを考えます.図8のように,球を水平に薄く切り,球の 中心から高さhにある厚さdhの薄い円盤の慣性モーメン トをi(h)とします.この円盤の半径がr(h)= R2 −h2 で与えられることから,式(13)より,この円盤の慣性モー



教えてください Okwave


慣性モーメント 物理学解体新書
X132 慣性モーメントの例 M (a) a (b) 図132 (a)円環(b) 円板 0 z ã a a z 2 2 aa 図133 球の慣性モーメント 図131(b)のように,棒の端点の周りの慣性モーメントは I = ∫ l 0 ˆx2dx = Ml2 3 . (138) 棒の中心の周りの慣性モーメントの方が小さい.一般に慣性モーメントは回転7 穴あき円盤の慣性モーメント 8 円盤の慣性モーメントについて質問です 9 この物理学の問題を解いていただきたいです。 よろしくお願い致します。 密度ρが一様で厚さがtの板から 10 半径Rの球内に一様に密度ρで電荷が分布している。このときの球外部の剛体の回転運動、慣性モーメント 61 剛体の回転運動 剛体の運動は、並進運動と回転運動にわけられる。ヒトの身体が関節まわりの回転運動を行うこ とや、スイング動作といった回転を基本としたスポーツ運動を考える上で、回転運動を理解してお くことは重要である。 図61にあるように物体


質量慣性モーメント 円柱 円盤 細い棒


剛体の運動
慣性モーメントは円盤の静的特性として重要な 要素であり,飛行挙動に極めて重要な影響を与え ると考えられる。試料円盤の慣性モーメントを表 3に示す。比較のために,前田(i995) が測定し た値を表4として示した。前田の報告では, 2本 吊り法を用いて一般男子用と女子用の円盤につい て



すべてのカタログ すごい 円盤 慣性 モーメント



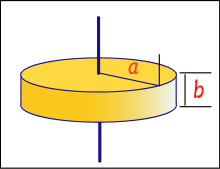
慣性モーメントの問題について 図のような外半径a 内半径bの中空円板 物理学 教えて Goo



中空円盤の慣性モーメント
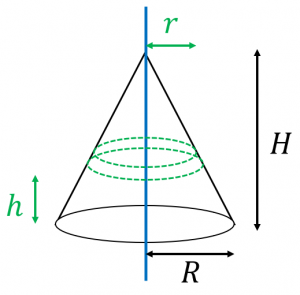


一様な円柱と円錐の慣性モーメント 具体例で学ぶ数学


色々な物体の慣性モーメント1 物理のかぎしっぽ
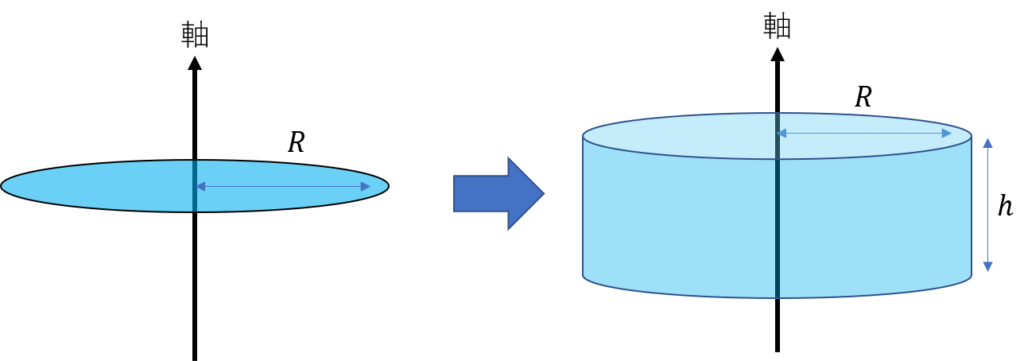


物理 慣性モーメントの計算の基礎を5種類の物体でわかりやすく解説
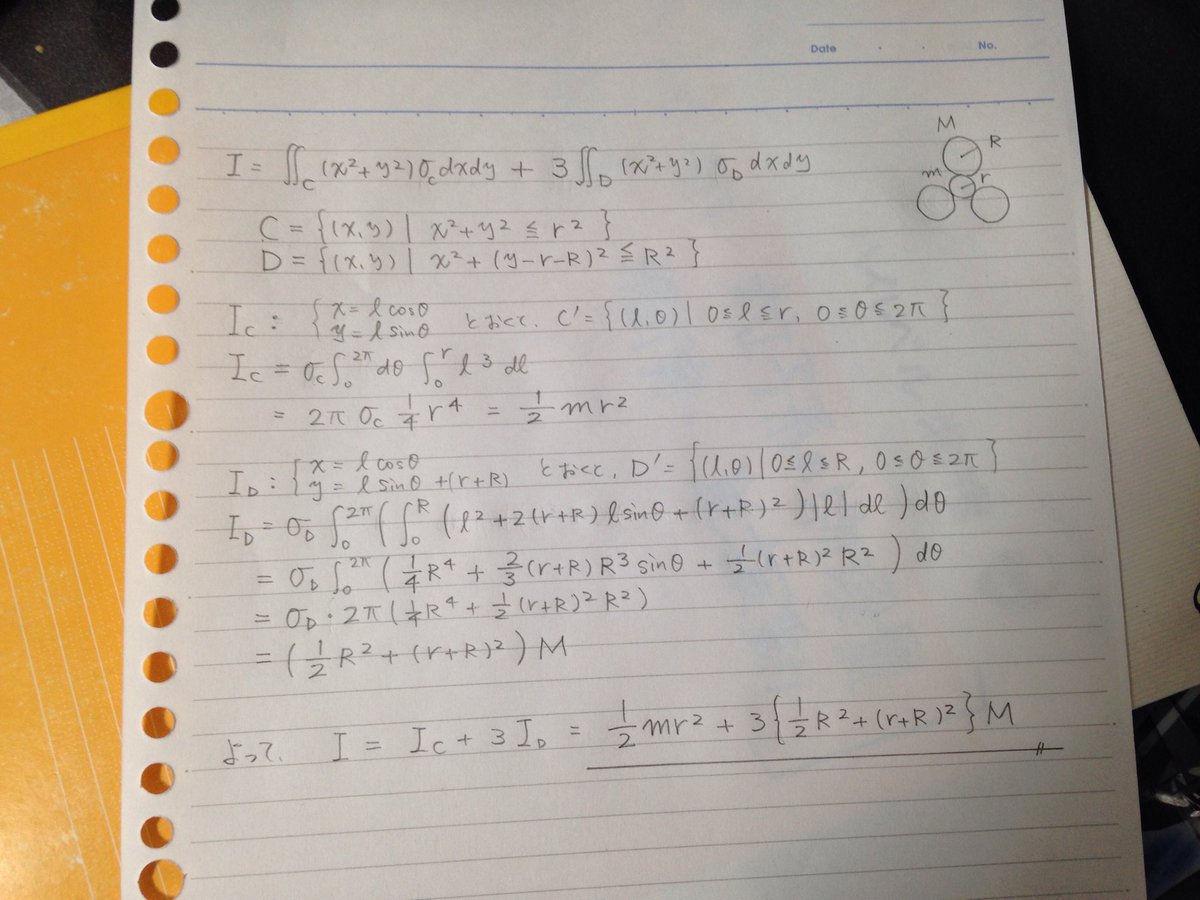


結数 ゆず على تويتر はい 等質量の円柱と円盤の慣性モーメントが等しいので ハンドスピナーを円盤の組み合わせに見立てました なのでsは面密度ですね 数学ガール大好きでいつも楽しませて頂いてます
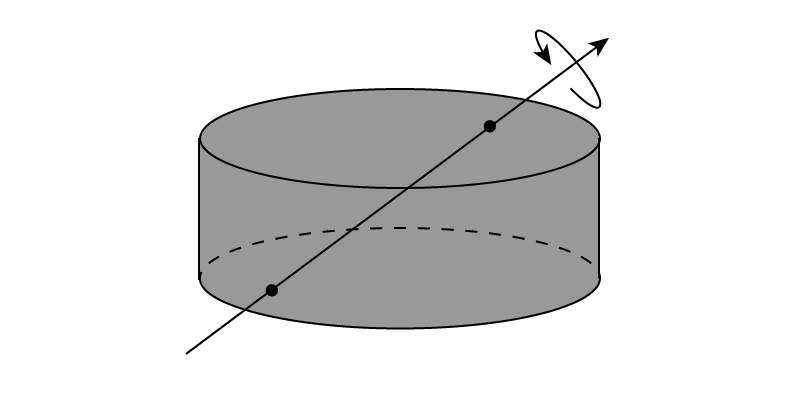


剛体の慣性モーメントの計算 物理の学校



期末テスト 1 日時 1月26日 木 4 5限 試験時間 90分程度 2 場所 1331番教室 Ppt Download


機械設計 有限会社オービット 慣性モーメントの計算例


質量慣性モーメント 円柱 円盤 細い棒



物理の問題 慣性モーメントなど です 物理の問題 慣性モーメントな 物理学 教えて Goo



力学 慣性モーメントは座標変換してから求めるべし ヨッシーの日記



物理 慣性モーメントの計算の基礎を5種類の物体でわかりやすく解説
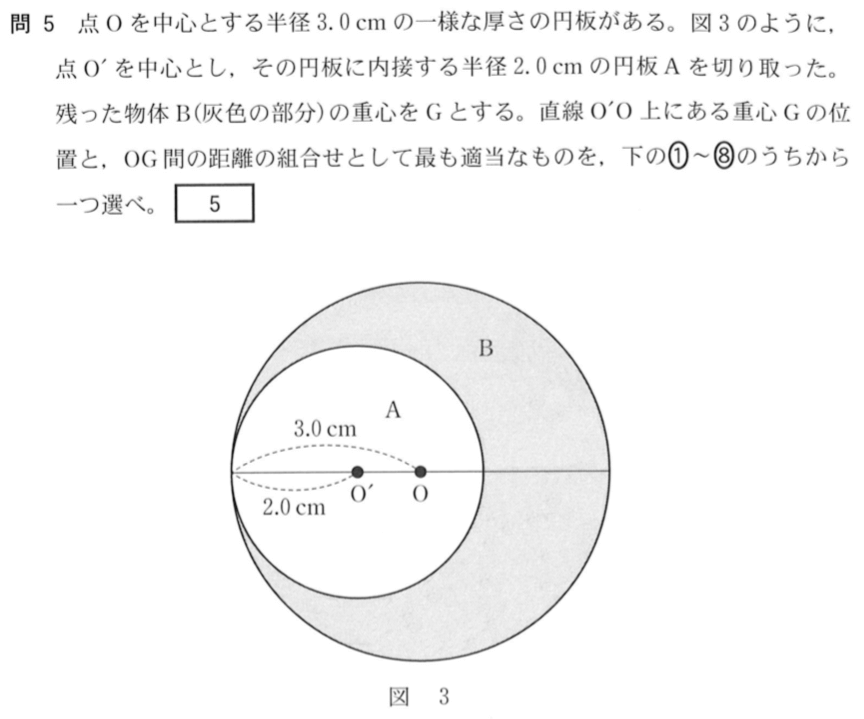


センター18物理第1問 問5 くり抜いた円板の重心 理科が好き Com


一様な物質でつくられた半径a 質量mの薄い円板がある 円板の中心からa Yahoo 知恵袋
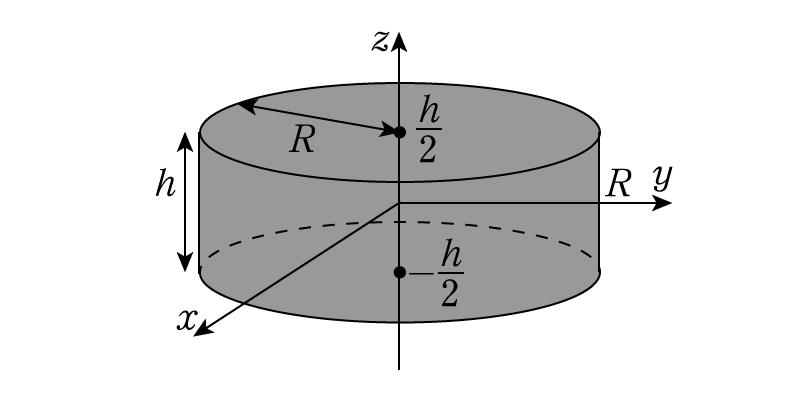


剛体の慣性モーメントの計算 物理の学校


剛体の運動 数学活用大事典



円柱と円盤の慣性モーメント Okwave


剛体の回転角の話 Yukiko Omori



直交軸の定理 1 Youtube


一様な球の慣性モーメント
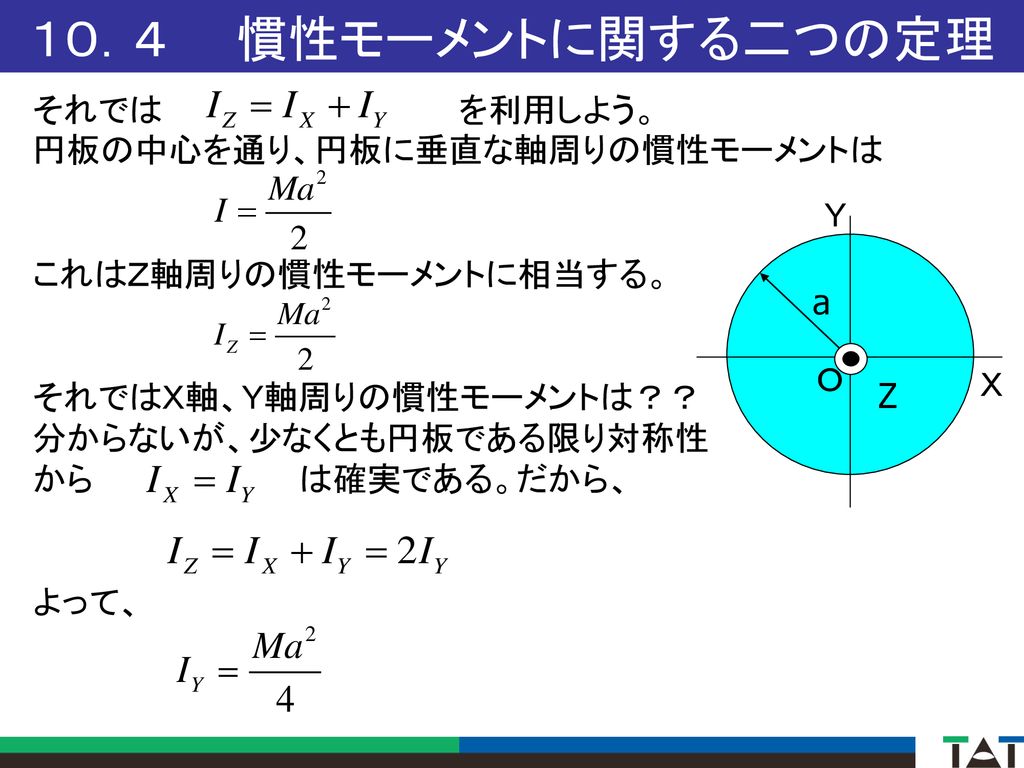


電気電子工学科e2 物理学基礎 物理学基礎演習 中間テスト問題 Ppt Download



円盤の慣性モーメントが求めれません Okwave


総合カタログ



慣性モーメントの公式慣性モーメントのとこ 物理に関する質問 勉強質問サイト



力学 円盤x軸まわり慣性モーメントを求めてみた プログラミング日記
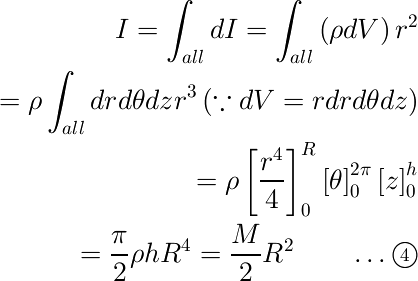


物体の回転 大学物理入門 A Guide For University Physics



M Sudo S Room 一様な円板の慣性モーメント 中心軸沿い


リング状の物体の慣性モーメント 物理学解体新書



電気磁気工学を学ぶ 長方形円板の慣性モーメント



剛体 半円板の運動と周期を求めてみた プログラミング日記


慣性モーメントを計算する Emanの力学



円盤の慣性モーメント


回転運動の運動方程式
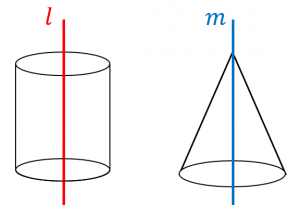


一様な円柱と円錐の慣性モーメント 具体例で学ぶ数学



工業力学入門講座 第回 剛体の慣性モーメント


物理の問題で 質量m 半径r円盤の中心を通り 円盤の面内にある回転軸の周 Yahoo 知恵袋



慣性モーメントj Kg M 2 の計算式 技術資料 オリエンタルモーター株式会社



点からリング ディスク 球までの慣性モーメントを見つける


やさしい実践 機械設計講座
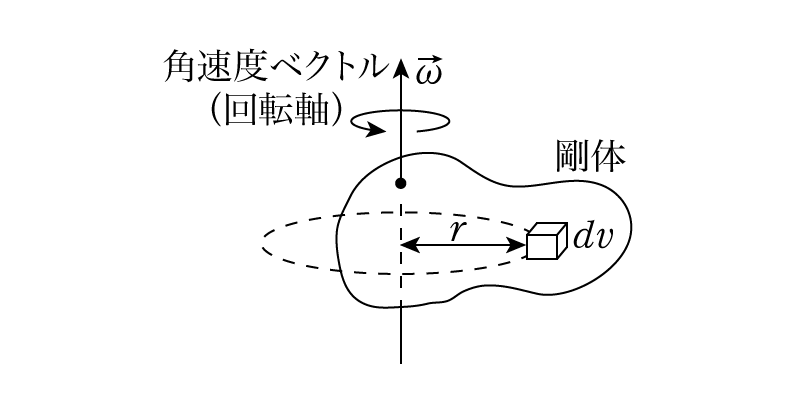


剛体の慣性モーメントの計算 物理の学校



電気磁気工学を学ぶ ヨーヨーの運動方程式


質量慣性モーメント 球 球殻 薄肉球殻


名古屋市科学館 科学館を利用する 展示ガイド フロアマップ 転がる円盤



円輪の慣性モーメント



力学 半円板の重心と慣性モーメントを求めてみた プログラミング日記



円の切り抜き図形の重心の求め方 公式 そんなの使わんよ 受験物理 Set Up



この物体の慣性モーメントの求め方が知りたいです Okwave


回転運動の運動方程式
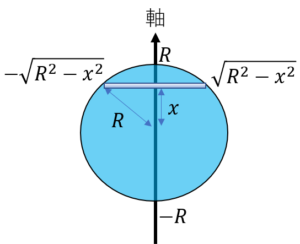


物理 慣性モーメントの計算の基礎を5種類の物体でわかりやすく解説



力学 ばねと円盤 物理に関する質問 勉強質問サイト


色々な物体の慣性モーメント1 物理のかぎしっぽ
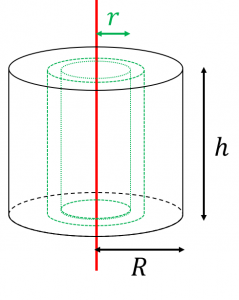


一様な円柱と円錐の慣性モーメント 具体例で学ぶ数学


色々な物体の慣性モーメント1 物理のかぎしっぽ
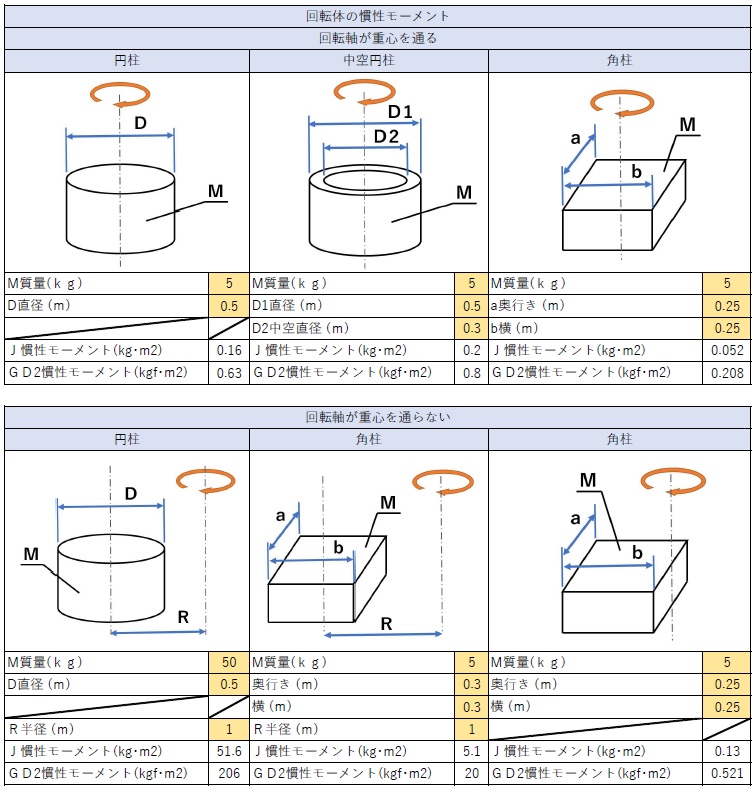


回転体の慣性モーメント イナーシャ の計算方法と計算エクセル


回転運動の運動方程式


大学物理張力慣性モーメント円盤ネットに上がってる解が掲載されていない Yahoo 知恵袋


剛体の回転角の話 Yukiko Omori
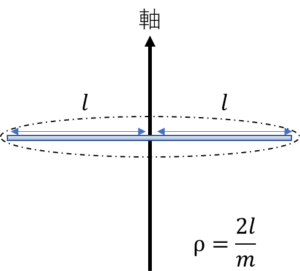


物理 慣性モーメントの計算の基礎を5種類の物体でわかりやすく解説



この物体の慣性モーメント こんにちは いつもお世話になっております 物理学 教えて Goo
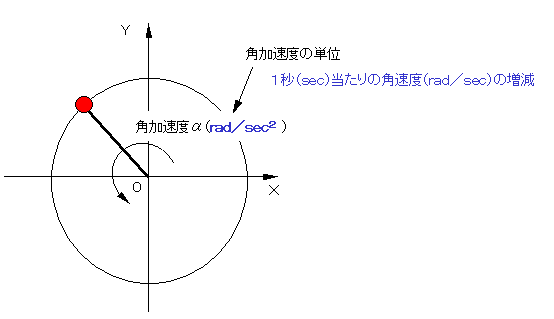


工業力学入門講座 第19回 回転運動の運動方程式



円柱の慣性モーメントの公式 円盤や球体の慣性モーメントの求め方まで


剛体の運動 数学活用大事典
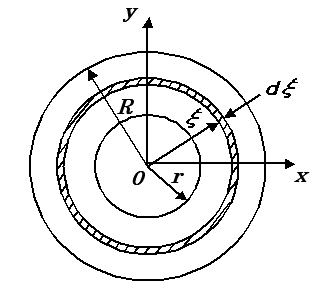


工業力学入門講座 第21回 連続体の慣性モーメント


円柱型の慣性モーメント 物理学解体新書



円柱の慣性モーメント
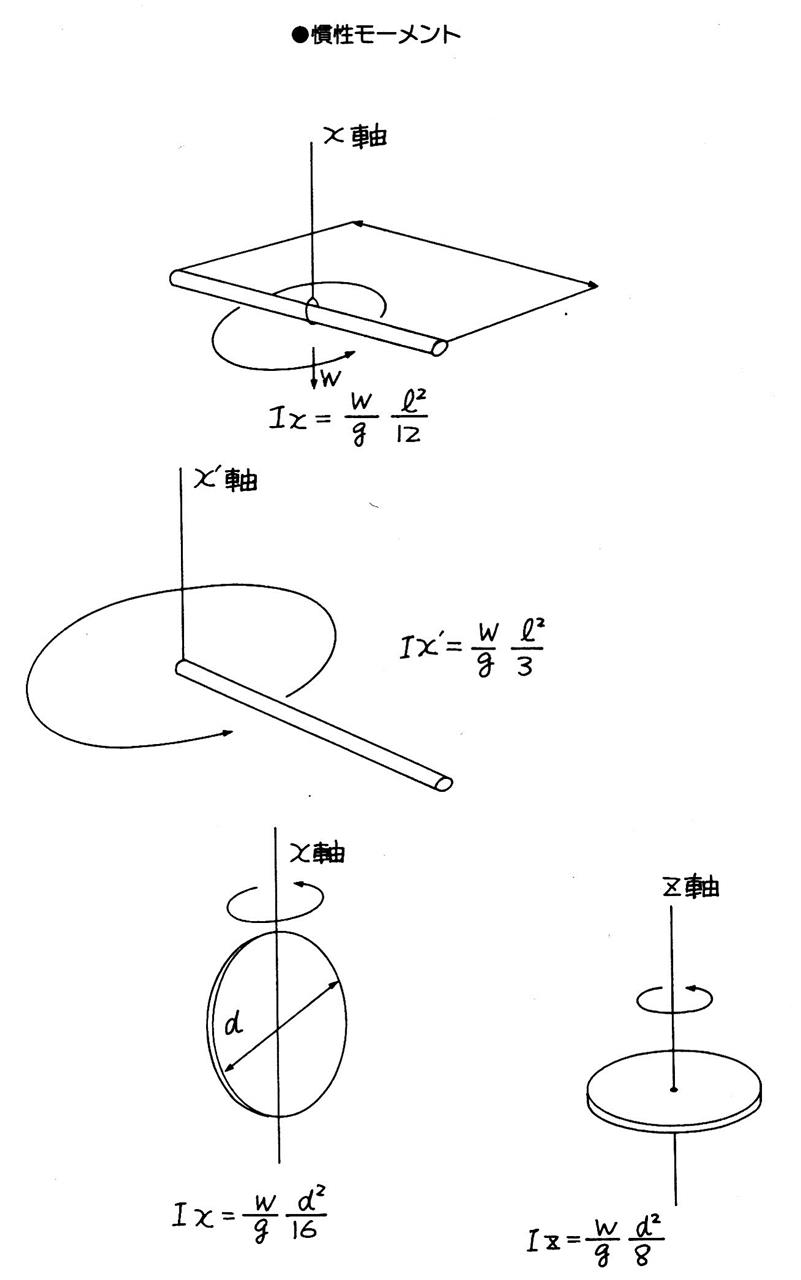


円盤 慣性 モーメント


コメント
コメントを投稿